¡Saludos y bienvenidos! Hasta ahora he abordado el cálculo de solicitaciones, sobre todo a través de la elaboración de sus respectivos diagramas, de miembros de eje recto. Esto tiene su aplicación a elementos estructurales reales tales como vigas o columnas.
Sin embargo, en la vida real podemos observar estructuras con elementos curvos. En esta publicación veremos cómo abordar estos elementos, donde aprendemos los métodos base para su análisis.
Introducción |
Esta publicación abordará el análisis de sistemas isostáticos compuestos por un solo miembro de eje curvo. Los principios que rigen este análisis son los mismos que se dan para miembros lineales, pero con la diferencia de que dichos elementos requieren de un análisis adicional debido a su configuración geométrica.
Las cargas externas son las mismas que hemos venido presenciando: fuerzas puntuales, cargas distribuidas o momentos externos. La diferencia radica en que el eje del elemento donde se aplican varía en su curvatura, haciendo que las solicitaciones se comporten de manera distinta respecto a un miembro lineal.
Quizás el lector haya escuchado con anterioridad que los arcos trabajan bajo esfuerzos de compresión. Esto es una característica que los hace ideal para resistir grandes cargas, debido a que materiales como el concreto y la roca resisten muy bien la compresión. Es por ello que observamos arcos en gran cantidad de estructuras antiguas y contemporáneas.

Miembros curvos. Generalidades |
Un miembro curvo o arco, se puede definir como una estructura de eje directriz no recto, la cual tiende a estar solicitada por fuerzas de compresión al someterse a cargas externas [1]. Estas cargas externas, por lo general, son debidas al peso propio del arco o a cargas superiores que actúan sobre él.
Una carga vertical dirigida hacia arriba tendería a generar tensión (tracción) en el arco. Sin embargo, esto no es muy común, por ello se dice que los arcos generalmente están sometidos a compresión. En este artículo nos referiremos a arcos cuyos apoyos se encuentran por debajo de él (en forma de “U” invertida).
Ejes locales y solicitaciones
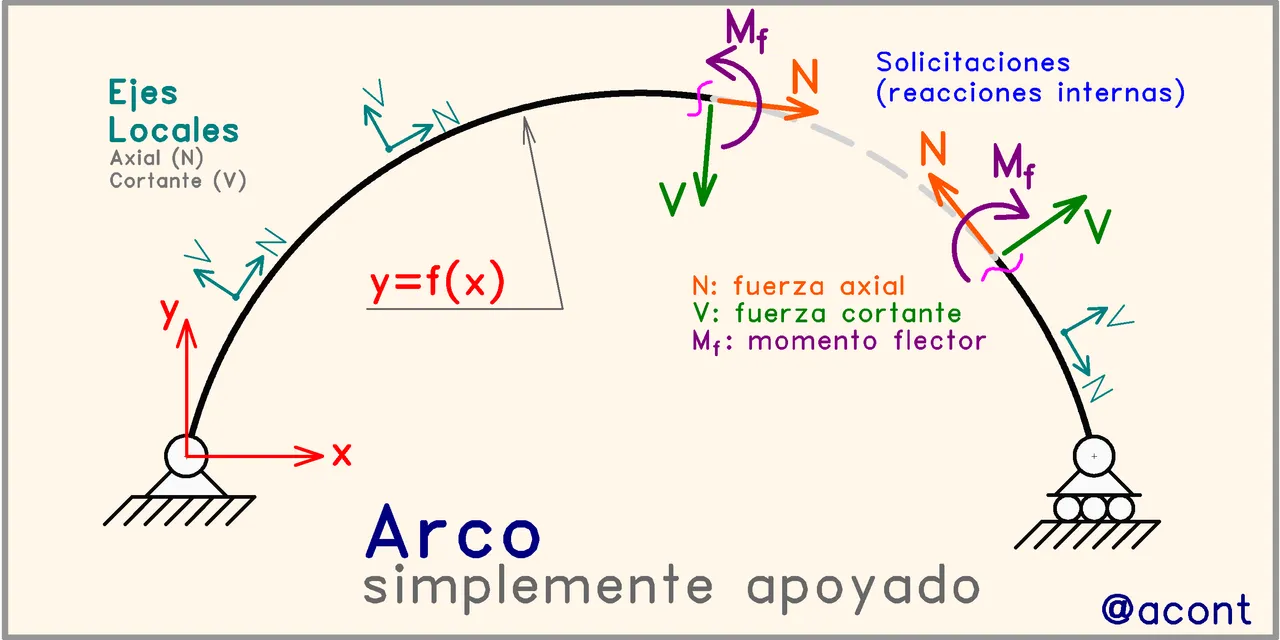
En la imagen anterior, podemos observar un arco simplemente apoyado. Los ejes locales se orientan de acuerdo al punto donde se encuentran. La fuerza axial “N” siempre será tangente al eje del miembro. La fuerza cortante “V” se orienta perpendicular a la tangente.
El momento flector Mf será horario o antihorario dependiendo de las cargas actuantes.
Discontinuidades
Al igual que como ocurre en miembros rectos, la presencia de distintas cargas externas genera discontinuidades o saltos en la ley matemática que define la magnitud de las solicitaciones.
En miembros curvos, se hace poco práctico emplear el método de integrar sucesivamente la ecuación de la carga externa, debido al comportamiento curvo. Por ello se hace necesario la realización de cortes y el empleo de las ecuaciones de equilibrio estático.
En la siguiente figura se ilustra un caso genérico:

Cortes y empleo de ecuaciones de equilibrio
Las cargas externas que están presentes en la figura establecen discontinuidades, generando a su vez distintos tramos o intervalos. En cada tramo o intervalo, se debe realizar un corte para hallar la ecuación que define tanto a las reacciones internas en horizontal y vertical, como al momento flector:
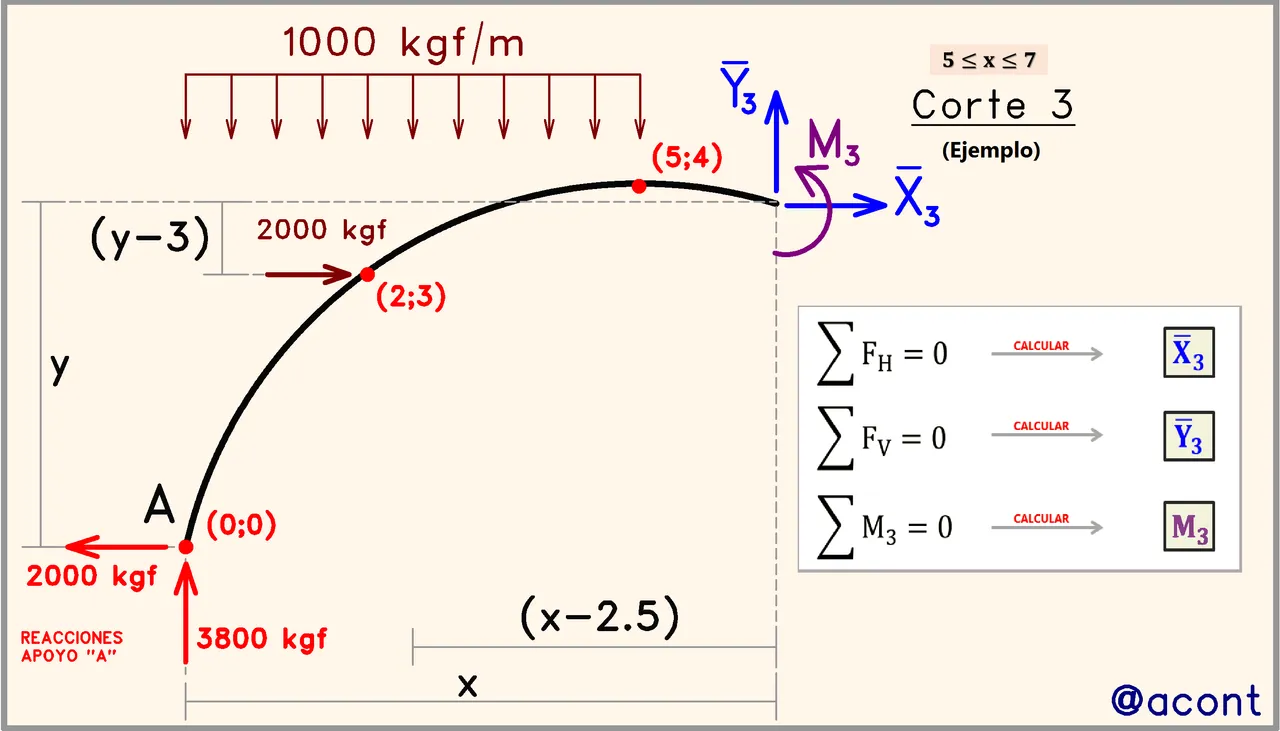
En la figura se realiza un corte en uno de los tramos (el tercero), ilustrando el procedimiento a realizar (sumatoria de fuerzas y momentos).
Cálculo de solicitaciones
El momento flector lo hemos hallado tal cual, pero debemos hallar la fuerza axial (N) y la fuerza cortante (V).
Una vez halladas estas reacciones internas generales (horizontal y vertical), podemos emplear las ecuaciones de transformación geométrica para pasar del sistema de ejes generales a ejes locales. En esta publicación, puedes encontrar material detallado referente a estas ecuaciones de transformación y su uso.

Con respecto a los valores de Sen(φ) y Cos(φ), los podemos hallar calculando el valor de “φ”. Este ángulo se calcula conociendo la pendiente de la curva. La pendiente de la curva no es más que la derivada de la función f(x) que la define.
Con esto en mente, podemos realizar una tabulación de todos estos valores para distintos puntos separados una distancia horizontal determinada (por ejemplo, cada @0.50 metros en horizontal).

Se podría incluso, simplificar esta tabla de la siguiente manera:

Para ello se deberán construir las ecuaciones de N. V y Mf manualmente, todas en función de ”x”. Un proceso que en un principio puede parecer complejo y poco práctico, pero nos ahorra una cantidad importante de dígitos intermedios en la tabla.
Primero, debemos expresar los valores de Sen(φ) y Cos(φ) en función de la pendiente, la cual a su vez representa a la derivada y=f(x):

El triángulo conformado por la pendiente de la tangente en cualquier punto nos ayuda a determinar Sen(φ) y Cos(φ) en función de sus catetos. Recordemos que dependiendo del cuadrante donde se encuentre el extremo del elemento, tendremos distintos signos para los valores de Sen(φ) y Cos(φ).
Siempre tendremos un signo negativo precediendo a las ecuaciones dadas. Cuando el corte se realice en un punto del arco con pendiente negativa, el signo cambiará de forma automática ya que la derivada y’ será negativa.
Introduciendo estas ecuaciones halladas en las ecuaciones de transformación geométrica, obtenemos ecuaciones generales para el cálculo de la fuerza axial y la fuerza cortante en cualquier miembro curvo:

Todos los parámetros incluidos en estas ecuaciones generales se pueden expresar en función de ”x”. Es decir, la distancia horizontal medida desde el origen del arco.
De esta manera hemos concretado la parte teórica del cálculo estructural de miembros curvos. Solo nos queda aplicar todo esto en un abordaje práctico, realizado a ejercicios dados por arcos circulares y parabólicos. Estas son las funciones matemáticas que podemos darle una aplicación más didáctica en ejercicios de arcos estructurales, los cuales abordaré en las próximas publicaciones.
Aportes de esta publicación
| Se comparte contenido relacionado al análisis estructural de miembros curvos, donde se proporciona un método de cálculo tabulado que permite conocer la magnitud de las solicitaciones a lo largo de todo el elemento curvo. Se establecen, además, ecuaciones generales para el cálculo de solicitaciones en miembros curvos, que permiten relacionar todas las variables geométricas y estructurales. De esta manera se introduce a la web a través de la plataforma HIVE contenido útil desde el punto de vista académico y técnico. |
Referencias
[1] Hibbeler, R. C. (2012). Análisis Estructural. Octava Edición. PEARSON EDUCACIÓN, México. (p. 194-195).Fuente
[2]Rodríguez, Iván. (2003). Estática de las Estructuras. (p. 124-133).Fuente
Material recomendado
•Estática Aplicada: transformación de reacciones al sistema local en barras inclinadas
•Las Ecuaciones de Equilibrio Estático y algunas aplicaciones en la Ingeniería Civil
Imágenes de autoría propia realizadas mediante LibreCAD y Microsoft PowerPoint. Tablas elaboradas mediante Microsoft Excel.
Publicado mediante la dApp STEMsocial |
Visite la comunidad StemSocial y las etiquetas #STEMsocial y #STEM-espanol para encontrar contenido de calidad referente a Ciencias, Tecnología, Ingeniería, Matemáticas (STEM por sus siglas en inglés) y otros tópicos relacionados. STEMsocial es una comunidad con cuatro años de trayectoria, conformada por autores de todo el mundo, en la que se comparte y apoya la difusión de contenido STEM en la web.
| Invitación al servidor de Discord de STEM-espanol: https://discord.gg/UJwQXWP | Registro en Hive |