Preface
In this series of posts, inspired by a lecture course given by Dr. Stephen Lynch, we will develop an understanding of the concepts that underpin the field of modern quantum optics. While some of this treatise is mathematical, it is my hope that this work will bring value to readers of all abilities. Before we delve deeply into quantum optics, we will examine the results of classical optics and review its limitations, as well as reviewing the progression of non-linear optics through the 1960s.

Introduction
We can partition the study of optics into three broad categories:
- Classical Optics - The interaction of 'ordinary' light with matter.
- Non-linear Optics - Light-matter interactions where the response if non-linear. This requires light of great intensity and large numbers of photons.
- Quantum Optics - The 'quantum nature' of light - small numbers of photons. It is in this category where photon statistics are important.
We begin this series by discussing the equations of the brilliant Scottish theoretician, James Clerk Maxwell.
Maxwell's Equations
Maxwell effectively took everything that was known about electromagnetism, at the time, and distilled it into four elegent equations. All of electromangetism is 'hidden' within these equations. In differential form, they are gven by
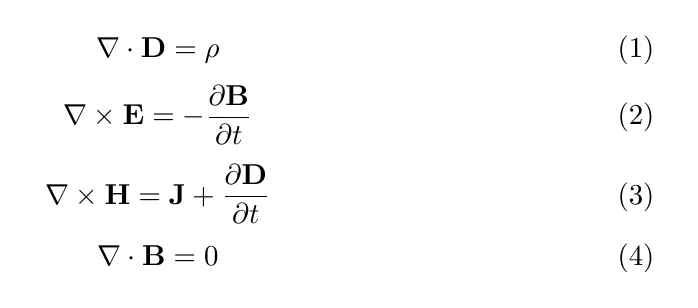
where

Equation (1) describes Coulomb's law, which states that the divergence of the electric field within a material is the charge density, and equation (4) describes the fact that magnetic field lines come in loops - the divergence of the magnetic field is zero.
Whenever you have a charge (which is a source), field lines emanate from it. The force law that comes with the charge is Coulomb's law. If we think about field lines crossing a given area, then we get Gauss's law, which describes the flux crossing the closed surface surrounding the charge, given by

Faraday's law of induction (2) describes the induced electromotive force (EMF) in any closed loop. Now, this EMF is proportional to the rate of change of the flux, with the negative sign a result of Lenz's law.
Ampere's law (3) states that a current generates a magnetic field.
The Wave Equation
Consider a vacuum, in which the charge density and current density are zero, and we make use of the vacuum permittivity and vacuum permeability. It can be shown through use of vector identities that

So what is the solution to this equation? Try substituting

You will see that this satisfies the wave equation, where the wave vector is given by

What Do Maxwell's Equations Give Us?
- The propagation of electromagnetic waves through matter depends on the permittivity and the permeability.
- In classical optics we usually confine ourselves to dealing with purely dieletric materials that have a linear permittivity i.e. no magnetic permeability.
- By treating electromagnetic radiation as a wave we can easily derive the laws of reflection and refraction which leads to ray optics.
- We can further study concepts like polarisation, interference, and diffraction.
Interaction of EM Radiation with Metals
- We can start by treating the treating the electrons and positive nuclear cores in the metal like a plasma.
- A plasma is most generally defined as gas of ionised particles.
- We usually associate plasmas with very high temperatures and energies (e.g. fusion) where electrons become separated from the nuclei of their atoms in the gas.
- However the key point is that it is an equal population of positive and negative charges, at least one of which is mobile.
Classical Light-Matter Interactions
The spatial separation of electrons from the positive atomic cores in the metal gives rise to electric dipoles. We now consider the effect of a small perturbing force. For small displacements, the restoring force is

We recognise the form of equation being analogous to classical simple harmonic motion. Once perturbed, an electron bound in this way will oscillate around its equilibrium position with a resonant frequency, given by the equation

where kE is the spring constant and me is the electron mass.
If we add in an electromagnetic perturbing force then the force experienced by the electron is given by

Now, summing the forces gives the 2nd order ODE

This is the equation for damped simple harmonic motion and we know the solution is of the form

Through substitution, it can be shown that in fact, we have
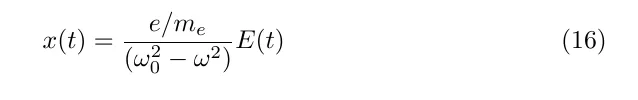
What are the implications of this?
We define the electric polarisation as

The dipole moment is the charge multiplied by the separation, thus for N electrons the permitivity is itself a function of frequency
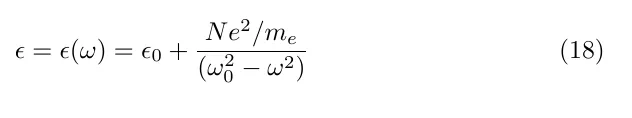
Along with the definition of refractive index, this defines a dispersion relation for the refractive index of a plasma
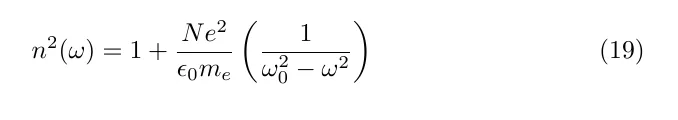
If we assume that w>>w0 and set Ne^2/e0 me = wp ^2 (the plasma frequency), so that
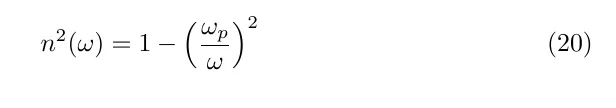
Below the plasma frequency the refractive index is complex, and the metal reflects electromagnetic radiation.
Above the plasma frequency refractive is real, and approximately = 1. In this regime the metal is transparent to electromagnetic radiation - i.e. metals become transparent at short wavelength.
In the next post, we will continue this discussion on classical optics.