Los números de Fibonacci son una de las sucesiones más conocidas por el público general, hasta son mencionados en películas de Hollywood. Estos números tienen muchas aplicaciones en diversas ramas de la ciencia y también en el arte y arquitectura; ya que las proporciones involucradas en la noción de belleza, están relacionadas con estos números.
Si denotamos por fn el n-esimo número de Fibonacci, estos están definidos por la relación de recurrencia fn+2=fn+1+fn, donde n es un entero no-negativo, y las semillas, o datos iniciales son f0=0 y f1=1.
Nos gustaría tener una fórmula cerrada o explícita para fn, es decir una que no involucre recurrencia. La respuesta se conoce como la Fórmula de Binet. Se le ha dado el nombre del matemático Francés Jacques Philippe Marie Binet (1786-1856), quien el 1843 la publicó. Aunque ya era conocida por Abraham de Moivre (1667-1754), Leonhard Euler (1707-1783) y Daniel Bernoulli (1700-1782).
La fórmula de Binet es:

Sin embargo hay una manera más elegante de expresarla, usando la razón dorada ( o también llamada razón áurea). La denotamos por Φ:
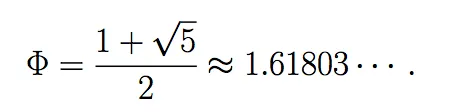
Recordemos que Φ es la raíz positiva del polinomio x2-x-1. Este polinomio está asociado a la relación de recurrencia de Fibonacci. Sea φ la otra raíz de es este polinomio.

La fórmula (1) escrita en términos de Φ y φ es

A continuación daremos una demostración de la fórmula de Binet.
Sea Zn=aΦn+bφn donde a y b son constantes. Mostraremos que Zn satisface la misma relación de recurrencia que la de los números de Fibonacci, es decir: Zn+2=Zn+1+Zn. Luego se encontrarán los valores de a y b tales que Z0=0 y Z1=1. De esta manera se demostrará la fórmula (2).
Como Φ y φ son raíces de la ecuación x2=x+1, las siguientes identidades se cumplen, para n entero no-negativo:

Por lo tanto:

Si se establece que Z0=0 entonces se tiene a+b=0. Similarmente, si Z1=1 entonces aΦ+bφ=1. De esta manera obtenemos el sistema de ecuaciones:

Su solución es:

Por lo tanto Zn=fn, demostrando así la fórmula (2).
Referencias:
https://en.wikipedia.org/wiki/Fibonacci_number#Closed-form_expression
http://mathworld.wolfram.com/BinetsFibonacciNumberFormula.html
https://en.wikipedia.org/wiki/Jacques_Philippe_Marie_Binet
T. Koshy, Fibonacci and Lucas Numbers with Applications, Wiley-Interscience, 2001.