Hi guys! I have a great news for you guys. I observed that my Visually Explained! article about Central limit theorem was a great success. And the point was it was less mathematical and focusing more on physical intuition. That makes sense. :) So I thought I will continue with the "Visually Explained Series" for different concepts. Today let us dive into Shannon's Entropy. I am sure that this journey is going to be really enjoyable.
For those who want to see my previous "Central Limit Theorem: Visually Explained!" article, click here.
Let us begin.

Source: wiki
From wiki again:
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, and cryptographer known as "the father of information theory".
Shannon's Information Entropy
Information theory is the study of quantifying, compressing, storing, communication, encoding, and decoding information. So what is Information? That is a great question!

It is not very easy to define information. But we can quantify information. Let us see how to deal this concept.
Think about a series of ones like below:
[1 1 1 1 1 1 1 1 1 1 .......]

Do you think this series of ones convey any "information"? I don't think so.
Nothing interesting right? I will say that this series conveys no information at all. Nothing surprising happens!
Let us compare 2 hypothetical news statements like these:
- (a) India wins football world cup.
- (b) India wins cricket world cup.
The second news item (b) is more probable to happen. Because India has a good cricket team. And in football, Indian rank is 150 I guess. So there is no chance for Indian football to even qualify for world cup. But if by chance India wins football world cup, then it has a more surprise element and hence one can say that statement (a) conveys more information content. Shannon thought about quantifying information and much more. And the result was the concept called Shannon Entropy and an entire subject called Information theory.
Let us come back to the sequence example. If there is a language which has only one symbol to type in, no information can be conveyed. Pretty obvious, right? Let us think about a language with 2 symbols. Let the symbols be 0 and 1. Let the probability to happen event '1' be Probability(1) a.k.a P(1). And let the event '0' occur with P(0).
The total probability P(0) + P(1) = 1, because some event (either 0 or 1) will happen. The information associated with an event is inversely related to the probability of that event. For example, take the statement India won the football worldcup. It is a very least possible event, right? The surprise element is higher. So we should treat information associated with the statement in an inverse manner. Least the probability, higher the information. Information is quantified as below:
Information corresponding to event 0 
I only told about inversion, where did the logarithm(base 2 because we are talking about 2 symbols) come from? One nice explanation comes from the fact that if you assign logarithm in the definition of information:
- When the probability of event 0 occurring is 1 (sure), the information content is zero. No surprise and so No information gained!
- Information must be quantity greater than or equal to zero. Some information is gained or nothing. Simple inversion i.e.
 will not satisfy this. Because if the probability is 1, the inversion will also be 1. We want it technically to be zero.
will not satisfy this. Because if the probability is 1, the inversion will also be 1. We want it technically to be zero.

- Another way to look at why logarithm comes is about asking YES/NO questions about predicting next symbol. How many YES/NO questions should we ask efficiently to predict the next symbol. The answer turns out to be a binary search. The order of complexity to find the next symbol thus follows a logarithm of total symbols. In an equiprobable scenario, the number of symbols will be inverse of the probability. It is explained here. The below youtube video will give you more insight:
Now we have a measure of information (which is related to the uncertainty of the occurrence of an event). But when you consider our sequence of ones and zeros, it is more sensible to talk about the average information content in the generated sequence. Say I have the below series of 1s and 0s.

There probability of symbols 0s and 1s:
- The probability of 0s, P(0)=32/60
- P(1) = 28/60
How do you get this? You can count the number of occurrence of ones/zeros and divide by total characters.
The information content
- Corresponding to 0s is:
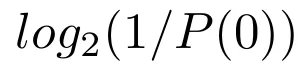
- Corresponding to 1s is:

Average Information content a.k.a SHANNON ENTROPY
How do you calculate average/mean E(x) of a quantity x with probability distribution P(x)?

So now our aim is to find weighted-average of information-content in the above series. This quantity is notated in literature as H(X). And it can be written as below:



Did you noticed the units of entropy is in bits, because we are talking about binary information(YES/NO question. And please note that any base system can be used in theory. But this makes things more sensible). The entropy is 0.9968 bits here.
What if we had equal ones and zeros in the sequence? Will there be more or lesser average information-content. I will say that it will have more uncertainty because you have the least clue here to predict next value in the sequence. If the probability of 1 to occur is higher than zero I can predict ones more time and I know more about the sequence because of lesser information content. So let us plot H(X) w.r.t. different probabilities P(1). P(0)=1 - P(1) since there are only 2 symbols. We will get some plot like below:
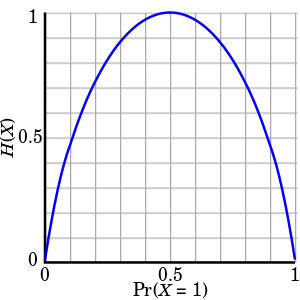
Source:Wiki
This essentially means that the uncertainty is higher if the symbols are equiprobable. As bias in distribution becomes higher, lesser the entropy and easier it to predict the next symbol.
This concept can be generalized to any kind of data, not necessarily sequences. It can be audio, images, video etc.
That's for now and bye! See you soon with a new topic. :)
References :
[1]: Communication Systems by Simon Haykins . Look for the chapter on Information Theory.
Hi,
@dexterdev here
Please Upvote and resteem my posts if you like my content.
I would like to hear your feedback. So please do comment those.
In case you have questions, please shoot those in comments.
All images without image sources are my creations :)
____ _______ ______ _________ ____ ______
/ _ / __\ \//__ __/ __/ __/ _ / __/ \ |\
| | \| \ \ / / \ | \ | \/| | \| \ | | //
| |_/| /_ / \ | | | /_| | |_/| /_| \//
\____\____/__/\\ \_/ \____\_/\_\____\____\__/

gif courtesy: @rocking-dave
