We have seen in a previous episode that matter–antimatter pair creation and annihilation should respect conservation laws. Yet, we only observe antimatter in minute quantities. Shouldn’t there be the same amount of each type around us?

And if there were, wouldn’t all matter and antimatter have already annihilated, leaving our Universe flooded with photons only?

Well, I have some partial answers to offer you.

First, we will travel through time from the big bang and witness how matter (and antimatter) came to be.

In a second section, we will discuss asymmetries in the behaviors of matter and antimatter, asymmetries which are actually observed experimentally. To really enjoy the trip, we will dive deep into one of the most fundamental theorems in Physics, The CPT theorem.

1/ Table of content and preliminary notes

To enjoy reading this post, you do not need a deep prior knowledge in particle physics (apart from the paragraph about CP violation). Yet, to fully understand all concepts presented, feel free to brush up a little by reading the previous articles first.

Episode 4A, “Antimatter, the mirror world” presents the fundamentals about antimatter.
Episode 4B, “Matter and Antimatter – An Explosive Couple!” dives into the interaction of matter and anti-matter (pair production and annihilation). Appendices are included at the end of this paper if you need a recap on particle physics fundamentals.
Episode 4C (this one) goes back in time instants after the big bang and witnesses the birth of matter and antimatter in the universe. It also explores matter/antimatter asymmetry and The CPT theorem.
Episode 4D will concern the detection of antimatter in our universe. Are there anti-planets, anti-stars and anti-galaxies?
Episode 4E will wonder if we could be the neighbors of an antimatter universe?

Now, let’s dive in!

2/ Witnessing the birth of matter and antimatter.

Let’s go back far in time, just a hundred thousandth of a second after the big bang.

The surrounding temperature is a staggering ten trillion degrees. Matter is under the form of a soup of quarks, antiquarks, gluons and photons with a density of around 100 million tons per cubic centimeter. Yet, this state does not last for long… The Universe is expanding and cooling rapidly. Soon enough, Quarks and antiquarks condense into protons and antiprotons.

But, already, anti-protons are at a deficit compared to protons… Antimatter is disappearing. The universe cools further, and the last anti-quarks take refuge into composite particles of lesser energy: mesons (assembly of one quark and one anti-quark). The latter do not stay stable for long, and by just a millisecond after the big bang, positrons appear to be the last remnants of antimatter…

The creation of electron-positron pairs requires less energy than that of quarks and antiquarks pairs, so leptons are still going through their genesis while the universe cools down at a temperature of around 10 billion degrees. The Universe is now 1 second old.

10 seconds later, the positrons go missing leaving only protons, neutrons and electrons.

We learned that, from energy, matter and antimatter are created in equal ways to preserve conservation laws. And then, when a particle and an antiparticle meet they annihilate releasing energy under the form of gamma photons.

Everything around us is obviously composed of matter. So where is the antimatter? Why such an asymmetry? Shouldn’t the universe be only made of photons (the product of matter-antimatter annihilation).

In order for you to follow the detective work of the scientists investigating this asymmetry, I need to introduce you to a concept called the CPT theorem.

3/ The CPT Theorem

When a fundamental theory or idea is proposed, there is a way to verify if it should be considered for further study or if it is just nonsense. See this like a kind of quality control protocol. The fundamental criterion to be considered is the in-variance of the proposed theory under certain symmetries. That means that if I apply a specific symmetry to a reaction the theory predicts and that is observed in nature, the resulting reaction should also be observable in Nature.

There are 3 fundamental symmetries that are to be considered: C (Charge), P (Parity) and T (Time reversal). The symmetry operators can combine, for example the CP operation consists in applying the C-symmetry and the P- symmetry simultaneously. The ultimate test for the invariance of a theory is to apply on it the CPT symmetry. It is not an easy concept to grasp, so let me give it a try by going into some details.

3.a - The Charge Symmetry

The charge symmetry is an operation where the electric charges of particles are swapped.

The C-symmetry transform the sign of a charge but not its magnitude. Consequently, the electromagnetic forces remain the same. Take two electrons, each charged negatively with the elementary charge -e. Place them close to each other: they repel each other with a given force.

Now apply the C-Symmetry to this system. Both particles will have the sign of their charge swapped to a positive charge +e. Other than this, nothing changes: they still repel with the same force...

You would expect that C-symmetry is always respected... Well, counter-intuitively, this is not the case. Not all reaction in our universe are C-symmetric.

3.2 - The Parity Symmetry

The parity symmetry is an operation where the directions in space are reversed: In the diagram below is represented the spin of electrons. the P-symmetry changes the direction of that spin from clockwise to anti-clockwise and vice-versa

Let’s see what we mean when we say that a reaction is P-symmetric. This symmetry appears obvious to common sense but is not that obvious when digging into small scale physics. Imagine a reaction occurring in nature. Say, two electrons have a trajectory such that they are approaching each other, while both moving from left to right. An exchange of photons between them will modify their momentum as in the drawing below.

If a reaction as seen in a mirror exists in nature, then it is said to be P-Symmetric. The P symmetric reaction involving our two electrons would correspond to the same phenomena but with the electrons moving from right to left this time…

I actually played around with a mirror...

You would expect P symmetry to be respected by all phenomena in nature. Again counter-intuitively this is not the case either.

3.3 - From Matter to Antimatter, The CP Symmetry

Now let’s check out what happens when I apply both C and P symmetry operations on a real particle.

As you may observe, combining C and P symmetries transforms our electron into... a positron, the anti-matter counterpart of the electron.

Consequently if nature respects CP symmetry, that implies that matter and antimatter should have a perfect symmetric behavior… thus be formed in the same amounts and in the end, completely annihilate each other… This is obviously not the case because we are here! So proving that not all reactions are CP symmetric is key in explaining the dominance of matter, thus our existence.

3.4 - The Time Reversal Symmetry

The time symmetry is an operation where the direction in time is reversed. Imagine you record on your fancy camera, an electron coming towards you while spinning clockwise. Then, you watch the movie in reverse: what you observe is the electron going away from you while rotating anticlockwise…

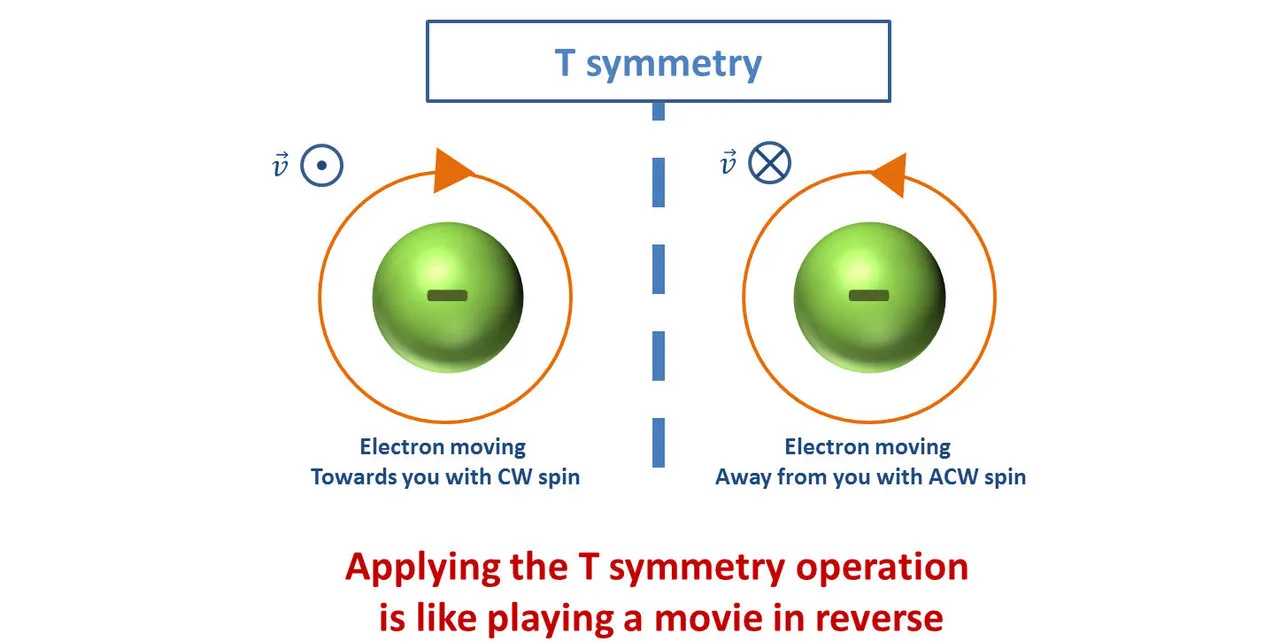
You can also think of what it means for a reaction to be T-symmetric. Imagine that you record with your video camera an interaction between particles: say two incident particles A and B with given momentum and energy meet up, interact and form two new particles C and D with their respective momentum and energy.

Now play your video backwards, you should observe particle C and D meeting up and as a result of their interaction, produce particles A and B with the same momentum and energy they had in the forward reaction. In addition, the probability of occurrence of the time-reversed reaction should match with that of the forward reaction.

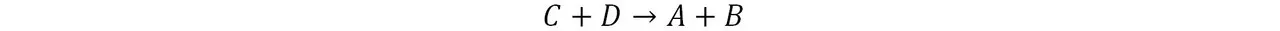
If such a time reversed reaction can be observed (or theoretically provoked) in nature, it implies that this reaction is T-Symmetric.

3.5 - The CP and T Symmetries are Complementary…

Here, I will make a wild approximation to illustrate a point (the specialists might jump out of their chair here ;-) ). We mentioned that T symmetry transforms a negative charge going towards you into a negative charge moving away from you: The latter can be considered equivalent as a positive charge moving toward you (the rate of change of the electric potential at the observer's position will be identical in both cases). This equivalence is massively used in electronics and electrical sciences. Thus we could approximate that the T symmetry transforms an electron into a positron.

Looks kind of familiar, don’t you think?

Yes, it looks furiously like the CP symmetry operation. Both CP and T appear complementary…

So combining all three C, P and T operations simultaneously ends up with an invariance: When applied on an electron spinning clockwise and going towards you, the CPT symmetry produces an electron spinning clockwise and going towards you :

This invariance of the CPT symmetry is a pillar in Physics. The violation of this symmetry has never been observed experimentally. If a theory does not respect it, then it is automatically invalidated.

It has been experimentally observed that Nature violates C and P symmetries. as well as CP and T symmetries. However, when CP is violated, it is accompanied by a violation of T which compensates so that CPT remains invariant.

The matter – antimatter unbalance is therefore possible without violating the most fundamental symmetries of all, the CPT symmetry.

3.6 - Experimental Proof of CP Violation.

We have seen in the previous paragraph that the dominance of matter over antimatter could be explained by the violation of CP symmetry. Such variation has been observed in multiple experiments.

The first indirect sign of such a violation was discovered in the asymmetry of oscillation of Neutral Kaons by Cronin, Fitch and Christenson.

There are two types of Neutral Kaons that naturally oscillate which means that they transform continuously from one type into the other.

In this oscillation process, a violation of CP symmetry occurs because the probability of a transformation from one type to another is slightly different than the reverse transformation.

A direct violation was experimentally observed experimentally much later in the 90s by looking at the decay of neutral Kaons into Pions. This involves a complex piece of theory, so I will need to bend a few lines here to make it easy to grasp for the non-initiated ;-). So again, my apologies to any specialist that happens to stumble across these lines.

As written above, the two types of neutral Kaons oscillate from one type to the other. As we are in the realm of quantum mechanics, there is an inherent uncertainty in knowing, at a given time, if a given Kaon is of one type or the other. The trick used here is to construct linear combinations of both states that then can be manipulated mathematically. This leads to the description of two new states for the particle labelled K1 and K2.

Roughly:

Kaons decay into pions. In order to respect CP symmetry, K1 particles can only decay into 2 pions (+ a lot of kinetic energy), and K2 particles into 3 pions (with little kinetic energy).

As you know from a previous episode, a decay is more probable when the product of a decay is of lower mass. Consequently, particles in the K1 state are shorter lived than particles in the K2 state by a large factor. This implies that K1 and K2 can be separated experimentally allowing them to be renamed K_short and K_longrespectively.

The experiment that was carried out in the nineties consisted in sending a beam of Kaons into a long tube, long enough for all the K_short to have decayed during the travel to the detector. Consequently, a pure K_long beam was produced.

It was observed that a small fraction of the K_long were decaying into 2 pions only. They should all be decaying into 3 pions. This phenomena violates CP symmetry...

Since then, more intense CP violating processes have been observed in the decay of B mesons (a Meson that contains a Bottom quark). A detailed article can be found here:
" The discovery of CP violation in B-meson decays " (Takasaki et al)

4/ So do we know now why matter dominates our observable universe?

Unfortunately, no… The experimental observations of CP violations could explain why matter dominates over antimatter, however, the degree at which CP violations occurs is much too small to explain the extent of the asymmetry between matter and antimatter. More asymmetric processes of much larger significance need to be found to explain why matter is predominant.

There is another option (here, beware: personal opinion!)…

Spacetime in our universe is measured flat at +/- 1%. This implies that what we observe is just a tiny sample of reality: The observable universe is most probably extremely small compared to the Universe with a capital U.

We cannot exclude that in other regions, forever hidden from us, matter is not the dominating type of matter present… We might just be mislead by a sampling bias, trying to find something (a fundamental asymmetry) that is just not there.

As we cannot observe what lies beyond the horizon of our observable universe, the apparent predominance of matter might be just an illusion. This is one of the ideas we will explore in the next episode!

So stay tuned!

The 'Particle Physics' series is aimed at providing an introduction to the world of small scale physics to non-scientists and high school students preparing for their high school exams.

Previous episodes:

Can't wait to know more?

If you can't wait to dive deep into the antimatter world, there are already some excellent articles on Steemit written by a professional particle physicist, @lemouth.

Sources, references and to dig deeper:

Image credits:

Big bang illustration (By NASA/WMAP Science Team (Original version: NASA; modified by Ryan Kaldari) [Public domain], via Wikimedia Commons (link)
All other pictures and visual elements are free for use commercially and were found either on Pixabay.
Scientific illustrations and diagrams produced by @muphy.
All illustrations, diagrams and friezes put together by @muphy using elements found on Pixabay.

Hi,
I’m @muphy (see intro post),
My life revolves around music production, teaching sciences, and discovery through travel.
You enjoyed that post? Resteem and Upvote!
You are interested in these topics? Follow me!

The Mystery of the Missing Antimatter - an Introduction to CPT Symmetry. (Particle Physics Series – Episode 4C)