Saludos y bienvenidos, vamos a entrar en el tema del análisis de la hiperestaticidad de sistemas materiales, viniendo de estudiar los criterios de estabilidad de sistemas materiales en el post anterior, se buscará con el presente explicar de forma didáctica y detallada los métodos para estudiar los grados de hiperestaticidad.
Todas las publicaciones sobre Estática Aplicada se han recopilado en la siguiente publicación:
•Material de Estática Aplicada
Para un mayor alcance de esta lectura se recomienda leer las siguientes publicaciones anteriores, donde se abordaron conceptos de importancia y otros aspectos sobre los cuales se fundamenta la presente publicación:
Introducción al Estudio de la Estática Aplicada: en este artículo se da una introducción al estudio de los sistemas materiales, se aborda el concepto de cuerpo rígido plano (chapa), un abordaje teórico-matemático de los grados de libertad y un breve análisis del estudio del equilibrio de una chapa a la cual se le añaden vínculos externos.
Estática Aplicada: los Vínculos y su Aplicación a Sistemas Estructurales en la Realidad: se describe detalladamente cada posible vinculación en el plano, tanto externa como interna, que pueden presentarse en el estudio de la Estática Aplicada y se explica brevemente cómo pueden ser usadas estas vinculaciones en estructuras reales.
Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación: se determinan algebraicamente los grados de libertad de un sistema material compuesto por un número “n” de chapas mediante una ecuación.
Criterios de Estabilidad de Sistemas Materiales en Estática Aplicada: se presenta la forma de clasificar los sistemas materiales de acuerdo a los grados de libertad que estos poseen.
Introducción
Al calcular los grados de libertad de sistemas materiales se deben determinar cuántas chapas posee el sistema, además de las unidades de vinculación tanto externas como internas existentes. El valor de los grados de libertad va a depender de cuantas vinculaciones existan, si resulta en un número negativo y se comprueba la no existencia de vinculaciones mal dispuestas (aparentes) entonces se dice que el sistema posee más vinculaciones de las necesarias para estar en equilibrio estático, es decir, hay un “exceso” de vinculaciones en el sistema material (de allí el prefijo “hiper“).
La hiperestaticidad puede darse externamente (respecto al sistema tierra) o internamente (cuando una chapa del sistema posee más vinculaciones entre barras de las necesarias para que la misma pueda considerarse un cuerpo rígido plano). El análisis de la segunda situación requiere que se deba considerar cada barra del sistema como una chapa y tomar en cuenta las vinculaciones que aportan las juntas rígidas. Esto puede ser un proceso poco práctico y largo si el sistema cuenta con una gran cantidad de barras vinculadas entre sí y una gran cantidad de vinculaciones internas a analizar, como es el caso de la Fig. N°1.

Para determinar los grados de libertad usaremos la Ecuación (3) del artículo *Determinación Algebraica de los Grados de Libertad de Sistemas Materiales en Estática Aplicada y Ejemplo de Aplicación:
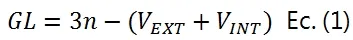
n=13 (barras AD, DI, DE, EF, IJ, FG, JG, BG, JK, GK, GH, HK, CH)
Vext=7 (empotramiento en A=3 + empotramiento móvil en B=2 + articulación fija en C=2)
Vint=40 (6 en D, 2 en E, 2 en F, 12 en G, 4 en H, 2 en I, 6 en J y 6 en K)
Aplicando la Ec. (1):
GL=3(13)-(7+40)=39-47=-8
Es decir, existen 8 vinculaciones además de las necesarias para garantizar la estabilidad del sistema material. De acuerdo al artículo Criterios de Estabilidad de Sistemas Materiales en Estática Aplicada en su Ecuación (2) obtenemos la siguiente relación entre los grados de hiperestaticidad y los grados de libertad:
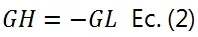
Entonces tendríamos 8 grados de hiperestaticidad. Se hace notar lo poco práctico del uso de esta ecuación para sistemas materiales con una elevada hiperestaticidad interna.
Método de los Cortes
Este método se basa en realizar cortes en el sistema material y estabilizar cada uno de los subsistemas creados añadiéndoles unidades de vinculación.

La idea es contar el número de vinculaciones eliminadas al realizar cada corte y contar el número de vinculaciones en total agregadas a los subsistemas para estabilizarlos.

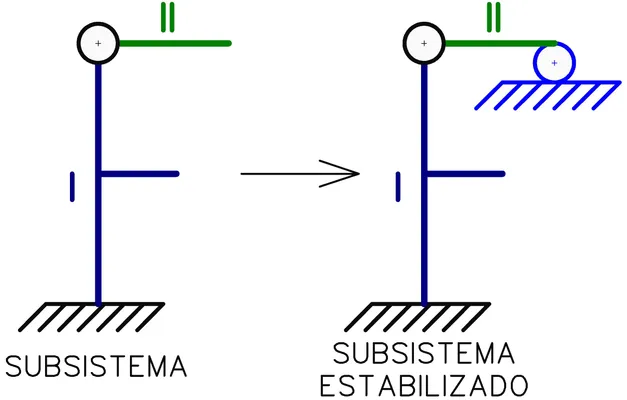
En el primer subsistema (Fig. N°4) generado por el corte 1-1 en la Fig. N°2, se observa que la chapa I está empotrada a tierra, por ende esta es estable y no requiere la adición de vinculaciones. Esto hace que la chapa II pueda rotar libremente alrededor de la rótula que vincula ambas chapas. Esta chapa puede estabilizarse restringiendo el movimiento vertical de sus puntos (perpendicular al radio de giro), y esto se puede lograr mediante un apoyo simple (rodillo en azul).
En el segundo subsistema que se ubica entre los cortes 1-1 y 2-2 (Fig. N°5), se observa que la chapa I tiene la posibilidad de presentar traslación horizontal respecto al sistema tierra (debido al empotramiento móvil), por lo tanto, esta chapa quedará estabilizada restringiendo su desplazamiento horizontal con un apoyo simple dispuesto tal como se ilustra. Así entonces, la chapa II necesita un rodillo que restrinja el desplazamiento vertical de sus puntos, ya que puede presentar rotación alrededor de la rótula que vincula ambas chapas.

El último subsistema posee tres chapas en total. La chapa I puede rotar alrededor de la articulación a tierra y para estabilizarla basta con colocar un rodillo que no permita el desplazamiento horizontal de sus puntos. La chapa II presenta la misma situación que la chapa II del primer subsistema, se le añade un rodillo que restrinja el desplazamiento vertical. Finalmente, al ser estables las chapas I y II, la rótula que las vincula con la chapa III se convierte en un centro de rotación para esta chapa y se debe evitar este movimiento colocando un rodillo que no permita a la chapa rotar.


Ya que al realizar un corte, es probable que los subsistemas presenten inestabilidades, al estabilizarlos con el número mínimo de vínculos se evidencia que en la estructura original existían más vinculaciones internas de las necesarias para garantizar el equilibrio estático interno. Por lo tanto los grados de hiperestaticidad serán simplemente la diferencia entre el número total de vinculaciones eliminadas (Velim) en el sistema original y el número total de vinculaciones agregadas (Vagr) a los subsistemas:
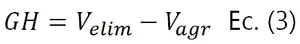
De esta manera podemos determinar de una manera más práctica los grados de hiperestaticidad del sistema mostrado en la Fig. N°1:
Ya vemos lo práctico del método para determinar los grados de hiperestaticidad internos de sistemas materiales, pero surgen las siguientes preguntas:
¿En qué criterio me baso para trazar los cortes sobre el sistema material?
¿Cuántos cortes debo hacer?
¿Por dónde trazo los cortes?
¿Cómo estabilizo los subsistemas?
Los cortes deben realizarse verificando que cada una de las subestructuras no presente hiperestaticidad interna, ya que así no se estaría realizando un análisis adecuado y el resultado que se obtendría no sería correcto. Se pueden realizar el mínimo número de cortes posibles con tal de analizar un menor número de subestructuras pero se debe cumplir con el criterio anterior.
La dirección de los cortes es aleatoria y en el caso de sistemas como el mostrado en la Figura N°1 se recomienda dejar un vínculo externo para cada subestructura. También es aleatoria la escogencia de la trayectoria de los cortes, se debe decidir si cortar un vínculo u otro o cortar sobre un punto aleatorio, como es el caso de la Fig. N°2, donde se optó por cortar la rótula en E, sin embargo se pudo haber cortado la rótula en F o bien haber realizado el corte sobre un punto cualquiera, esta escogencia puede afectar ligeramente el número de vinculaciones eliminadas y la forma de alguna u otra subestructura, pero no al resultado final.
Se suelen utilizar apoyos simples (rodillos) para llevar cada subsistema a la estabilidad, añadiendo el número mínimo de los mismos para cumplir dicho fin y además deben de colocarse de manera tal que aseguren la estabilidad del conjunto. Lo anteriormente dicho se refiere a que no tiene sentido colocar un rodillo sobre un chapa que ya es estable dentro del subsistema, tampoco lo es colocar un rodillo de manera que el mismo genere una restricción aparente (que no hace nada y no ayuda a estabilizar). Se puede usar la Ecuación (1) para determinar los grados de libertad del subsistema y de acuerdo al número obtenido se añade la misma cantidad de rodillos. También pueden utilizarse otros vínculos para estabilizar subsistemas (como veremos adelante), tomando en cuenta que no todos poseen una solo unidad de vinculación como en el caso del apoyo simple.
Veamos un ejemplo de análisis de hiperestaticidad externa e interna en un sistema material un poco más “irregular”:
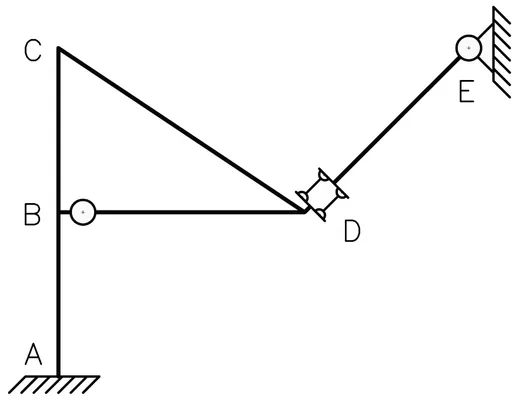
Podemos realizar un análisis de la hiperestaticidad externa tomando como chapa a todo arreglo de barras que vinculadas entre sí forman un cuerpo indeformable sin importar si existe hiperestaticidad interna (Como es el caso del arreglo ABCD en la Fig. N°8):
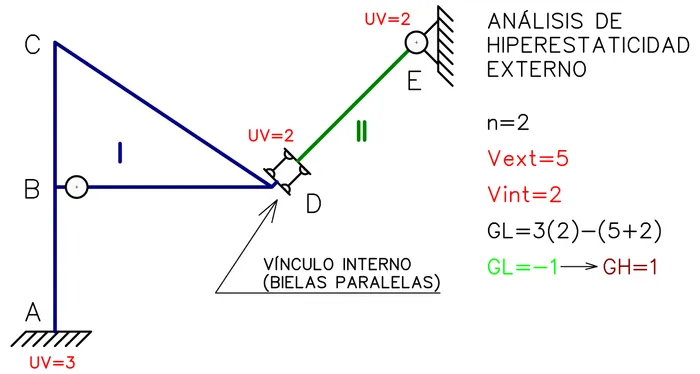
Para analizar la hiperestaticidad interna podríamos asumir cada barra como cuerpos rígidos y tomar en cuenta las vinculaciones rígidas internas, pero usaremos el método de los cortes.
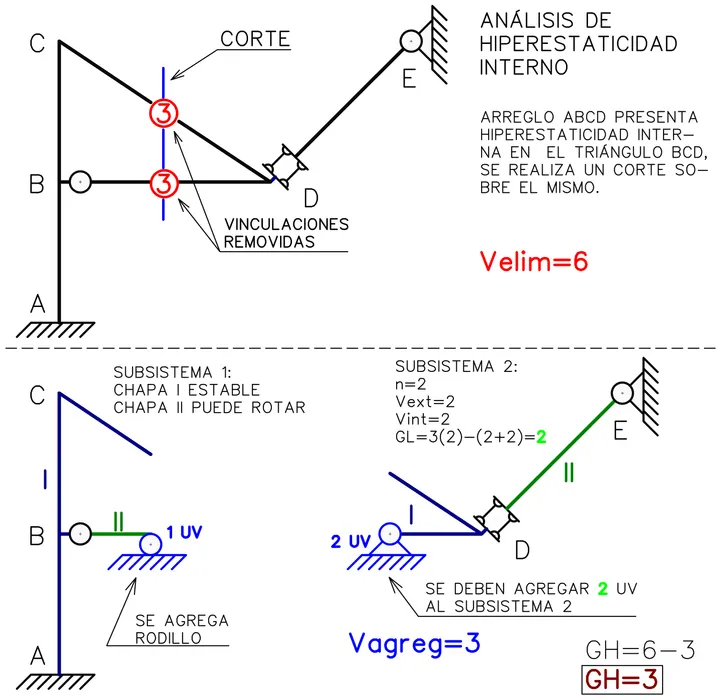
Finalmente llegamos a la conclusión de que el sistema material mostrado en la Fig. N°8 posee un grado de hiperestaticidad externa, pero internamente posee tres grados de hiperestaticidad.
Recordemos que un sistema material bien podría ser isostático o incluso inestable externamente pero presentar hiperestaticidad interna, o viceversa.
Aportes
Con este artículo se busca dejar una referencia sobre el tema dada la escasa bibliografía que se tiene al respecto y se realiza un aporte al estudio de este tópico de la estática de una manera concisa y didáctica.
Conclusiones
- El método de los cortes permite analizar la hiperestaticidad interna de sistemas materiales de una manera más práctica, sobre todo para sistemas con un gran número de barras y vinculaciones internas (hiperestaticidad alta).
- La hiperestaticidad interna se da cuando existe un número de vinculaciones internas más de las suficientes para asegurar la estabilidad del arreglo de barras y se evidencia al realizar cortes y estabilizar las subestructuras.
- La hiperestaticidad externa se puede estudiar con la ecuación usada para el cálculo de los grados de libertad asumiendo que cada chapa es todo arreglo de barras que logren conformar un cuerpo rígido plano.
- El método de los cortes no posee una manera fija de aplicarse y puede realizarse un análisis previo del sistema para observar cuantos y donde es más conveniente trazar los cortes con tal de no obtener subsistemas con hiperestaticidad interna.
Referencias Bibliográficas
- Rodríguez, Iván. (2003). Estática de las Estructuras. P. 34.
- Arroyo Roo, Alberto (1993). Análisis Estructural-Tomo II (Estructuras Hiperestáticas). Caracas, Venezuela. Fondo Editorial Lola de Fuenmayor. P. 12-14.
Imágenes y ecuaciones de autoría propia realizadas mediante LibreCAD y Microsoft Word por @acont.