In the last post we made a first attempt to describe how light interacts with matter. We treated the dielectric material as a plasma of electrons bound to positive atomic cores, and we disturbed the equilibrium by subjecting the electrons to a small electric field (weak EM wave). Then, by coupling this with Maxwell's equations, we were able to sucessfully predict the frequency dependence of refractive index.

UV Transparency of Alkali Metals
The dispersion relation implies that metals are transparent to high frequency radiation (e.g. X-rays). In order to show that alkali metals are transparent to UV light, we use the equation for plasma frequency,

This yields to a plasma frequency of ~5.7 x10^15 rad/s, corresponding to a wavelength of ~330 nm.
Electric Field from an Ideal Dipole
Suppose we have two opposite charges separated by a distance d, centred on the origin of coordinates. The first step is to write down the electrostatic potential which is the superposition of the potential for each charge.

Then, it is simple to show that
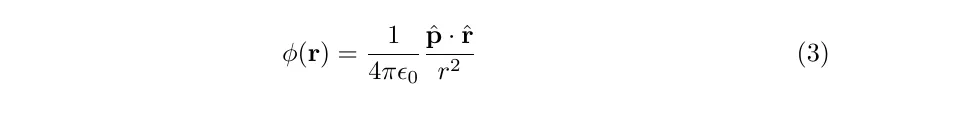
where p = qd.
Now that we know the electrostatic potential, we may take the gradient in order to determine the field
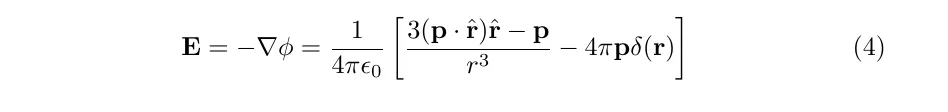
Note that the delta function in this expression does not contribute to the field far away from the dipole; its purpose is to ensure that the following volume integral is satisfied
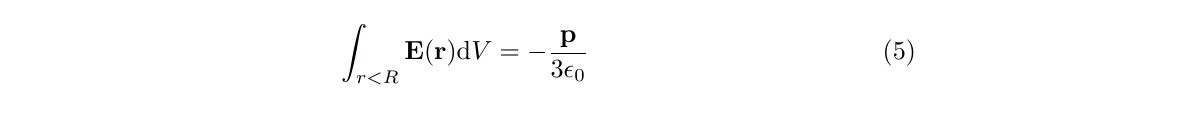
Any change in the distance between the two charges will result in a change in the magnitude of the dipole vector and the elctric field. This can lead to radiative emission of EM radiation.
Extension to Charge Density
We may write down the potential for several discrete charges as a sum
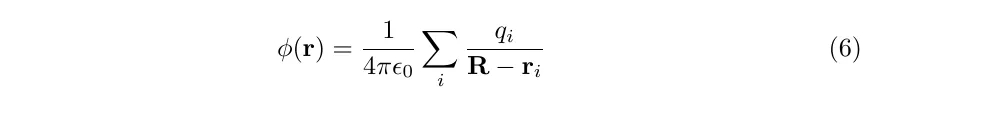
It is reasonable to extend this to a continuous charge distribution with a charge density rho(r)

We can expand the term in the denominator of (7) in a binomial expansion to yield
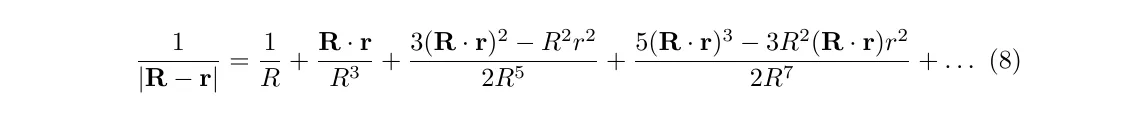
allowing us to write
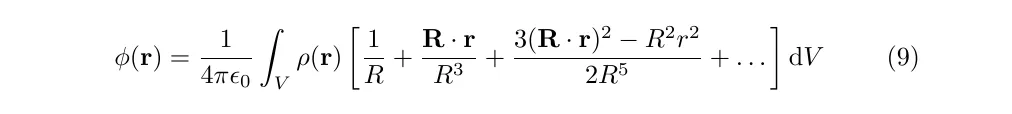
Summary
- Classical optics has given us an understanding of how light propagates through materials.
- This allows us to design lenses, mirrors, prisms, gratings, etc. as well as more complicated instruments which involve compound optics such as microscopes and telescopes.
- We also achieve a basic understanding of how light of different frequencies interacts with the electrons inside dielectric materials.
- We get a basic idea of how spatial separation of charge can lead to electromagnetic radiation.